Transistor math¶
import matplotlib.pyplot as plt # importar a bilioteca pyplot para fazer gráficos
import matplotlib.ticker as plticker
import matplotlib.colors as mcolors
import numpy as np # importar a biblioteca Numpy para lidar com matrizes
import pandas as pd # importa bilioteca pandas para lidar com processamento de dados
import os
from scipy import optimize
import SchemDraw as schem
import SchemDraw.elements as e
import matplotlib.colors as mcolors
from myst_nb import glue
def draw_transistor(unit_size, **kwargs):
d = schem.Drawing(unit=unit_size,**kwargs)
VB = d.add(e.DOT_OPEN, label='$V_{BB}$')
RB = d.add(e.RES, d='right',label='$R_{B}$')
bjt = d.add(e.BJT_NPN_C, d='right')
#----
Rc = d.add(e.RES, d='up', xy=bjt.collector, label='$R_C$')
Vcc = d.add(e.DOT_OPEN, label='$V_{CC}$')
#RE = d.add(e.RES, d='down', xy=bjt.emitter, label='$R_E$')
gnd = d.add(e.GND,xy=bjt.emitter)
return d
def plot_load_lines_transistor(Vcc=10,Rc=100,Vbb=1,Rb=1000):
def Ib(Vbe,Ies=3*1e-14):
β = 39.6 #[1/V]
return Ies*(np.exp(β*Vbe-1))
def Ic(Vce,Ies=300*1e-14, VEA = 200):
β = 39.6 #[1/V]
#VEA = 40 # Early Voltage
βr = 0.0001
αr = βr/(1+βr)
Vbc = Vbe - Vce
return Ies*( np.exp(β*Vbe-1)*(1+(Vbe-Vbc)/VEA) - 1/αr*(np.exp(β*Vbc)-1))
def Vdiodo(I,Is=1e-13):
β = 39.6 #[1/V]
return 1/β*np.log(1+I/Is)
def KVL(V,Vin,R):
return Vin-R*Ic(V)-V
def KVLb(V,Vin,R):
return Vin-R*Ib(V)-V
def Vdiodo(Vin,V0,R):
return optimize.brentq(KVL, -1.1*V0, 1.1*V0, args = (Vin,R))
def Vdiodob(Vin,V0,R):
return optimize.brentq(KVLb, -1.1*V0, 1.1*V0, args = (Vin,R))
#return fixed_point(lambda x: Vin-R*Idiodo(x)-x,0.6,args=(1.0,100))
npt=50
Vin = Vcc
Vb0 = Vbb
#---
fig_size = (18,6)
fig,ax = plt.subplots(1,3,figsize=fig_size)
#------------------
ax0 = ax[0]
draw_transistor(2.5).draw(ax=ax0)
ax0.set_aspect('equal')
#DivTensao([e.RES,'R'],[e.DIODE,'D'],fonte = [False,e.SOURCE_V]).draw(ax=ax0)
ax0.axes.get_xaxis().set_visible(False)
ax0.axes.get_yaxis().set_visible(False)
ax0.set_frame_on(False)
ax0.set_xticklabels(())
ax0.set_yticklabels(())
ax0.get_figure().set_size_inches(fig_size[0]*0.7,fig_size[1])
#------------------
#BASE
Vin_min, Vin_max = 0,2 # [V]
I_min, I_max = 0,1500e-6 # [μA]
I=np.linspace(I_min,I_max,npt)
V = np.linspace(0,1,npt)
Vlhs = Vb0-Rb*I # equação LHS
ax0 = ax[1]
ax0.plot(Vlhs,I*1e6,label = r'$V_{BB}-R_B I_B-V_{BE}(I_B)=0$')
ax0.plot(V, Ib(V)*1e6, c='r',lw=2, label = r'$I_B(V_{BE})$',zorder=4)
#solução para corrente e tensão
Vd = Vdiodob(Vb0,Vb0,Rb) # equação RHS
Id = Ib(Vd)
ax0.axhline(1e6*Id, c='k', ls = '--',zorder=0)
ax0.axvline(Vd, c='k', ls = '--',zorder=0)
lab = r'$I_B$,$V_{BE}$'+'={:2.0f} μA, {:2.0f} mV'.format(1e6*Id,1e3*Vd)
ax0.scatter(Vd,1e6*Id, c='r', marker='o', s=100, label=lab)
#---
#lab = '$V_{aberto}$'+'={} V'.format(Vb0)
ax0.scatter(Vb0,0, color='b', marker='o', s=70,zorder=3)
#lab = '$I_{curto}$'+'={:2.1f} mA'.format(1e6*Vin/Rb)
ax0.scatter(0,Vb0/Rb*1e6, color='b', marker='P', s=70,zorder=3)
#---
#eixos x-y
ax0.axhline(0, color='k', linestyle = '-',lw=2)
ax0.axvline(0, color='k', linestyle = '-',lw=2)
#-----------------------
ax0.set_xlabel('Tensão, $V_{BE}$ (V)')
ax0.set_ylabel('Corrente, $I_B$ (μA)')
ax0.set_xlim([Vin_min,Vin_max])
ax0.set_ylim(np.array([I_min,I_max])*1e6)
ax0.legend(loc = 'lower center',bbox_to_anchor=[0.5,1.0])
ax0.grid(True,which='both')
#------------------
#COLETOR_EMISSOR
Vbe = Vd # from previous
#limites dos eixos
Vin_min, Vin_max = -1,10 # [V]
I_min, I_max = -1,100 # [mA]
#-------------
V = np.linspace(0,10,npt)
#I = Idiodo(V) # equação diodo
I=np.linspace(I_min,I_max,npt)
#----------------------
Vlhs = Vin-Rc*I # equação LHS
#Vlhs = Vin-R*Id # equação LHS
#Vrhs = Vdiodo(Vin,Vin,R) # equação RHS
ax0 = ax[2]
ax0.plot(Vlhs,I*1e3, label = r'$V_{CC}-R_C I_C-V_{CE}(I_C)=0$')
ax0.plot(V, Ic(V)*1e3, c='r',lw=2,label = r'$I_C(V_{CE})$',zorder=4)
#---
#eixos x-y
ax0.axhline(0, color='k', linestyle = '-',lw=2)
ax0.axvline(0, color='k', linestyle = '-',lw=2)
#---
#lab = '$V_{aberto}$'+'={} V'.format(Vin)
ax0.scatter(Vin,0, color='b', marker='o', s=70,zorder=3)
#lab = '$I_{curto}$'+'={:2.1f} mA'.format(1e3*Vin/Rc)
ax0.scatter(0,Vin/Rc*1e3, color='b', marker='P', s=70,zorder=3)
#solução para corrente e tensão
Vd = Vdiodo(Vin,Vin,Rc) # equação RHS
Id = Ic(Vd)
ax0.axhline(1e3*Id, c='k', ls = '--',zorder=0)
ax0.axvline(Vd, c='k', ls = '--',zorder=0)
lab = r'$I_C$,$V_{CE}$'+'={:2.0f} mA, {:2.0f} V'.format(1e3*Id,Vd)
ax0.scatter(Vd,1e3*Id, c='r', marker='o', s=100, label=lab)
#-----------------------
ax0.set_xlabel('Tensão, $V_{CE}$ (V)')
ax0.set_ylabel('Corrente, $I_C$ (mA)')
ax0.set_xlim([Vin_min,Vin_max])
ax0.set_ylim([I_min,I_max])
ax0.legend(loc = 'lower center',bbox_to_anchor=[0.5,1.0])
ax0.grid(True,which='both')
ax0.xaxis.set_major_locator(plticker.MultipleLocator(2))
ax0.yaxis.set_major_locator(plticker.MultipleLocator(10))
#ax0.xaxis.set_major_locator(plticker.MultipleLocator(1))
#ax0.yaxis.set_major_locator(plticker.MultipleLocator(2))
plt.tight_layout()
return
def plot_ic_curves_transistor(Vcc=10,Rc=100,Vbb_vec=np.arange(0.6,1.8,0.3),Rb=1000):
def Ib(Vbe,Ies=3*1e-14):
β = 39.6 #[1/V]
return Ies*(np.exp(β*Vbe-1))
def Ic(Vce,Ies=300*1e-14, VEA = 200):
β = 39.6 #[1/V]
#VEA = 40 # Early Voltage
βr = 0.0001
αr = βr/(1+βr)
Vbc = Vbe - Vce
return Ies*( np.exp(β*Vbe-1)*(1+(Vbe-Vbc)/VEA) - 1/αr*(np.exp(β*Vbc)-1))
def Vdiodo(I,Is=1e-13):
β = 39.6 #[1/V]
return 1/β*np.log(1+I/Is)
def KVL(V,Vin,R):
return Vin-R*Ic(V)-V
def KVLb(V,Vin,R):
return Vin-R*Ib(V)-V
def Vdiodo(Vin,V0,R):
return optimize.brentq(KVL, -1.1*V0, 1.1*V0, args = (Vin,R))
def Vdiodob(Vin,V0,R):
return optimize.brentq(KVLb, -1.1*V0, 1.1*V0, args = (Vin,R))
#return fixed_point(lambda x: Vin-R*Idiodo(x)-x,0.6,args=(1.0,100))
fig_size = (18,6)
fig,ax = plt.subplots(1,3,figsize=fig_size)
colors=list(mcolors.TABLEAU_COLORS.keys())
for ii,Vbb in enumerate(Vbb_vec):
npt=50
Vin = Vcc
Vb0 = Vbb
#---
#------------------
ax0 = ax[0]
draw_transistor(2.5).draw(ax=ax0)
ax0.set_aspect('equal')
#DivTensao([e.RES,'R'],[e.DIODE,'D'],fonte = [False,e.SOURCE_V]).draw(ax=ax0)
ax0.axes.get_xaxis().set_visible(False)
ax0.axes.get_yaxis().set_visible(False)
ax0.set_frame_on(False)
ax0.set_xticklabels(())
ax0.set_yticklabels(())
ax0.get_figure().set_size_inches(fig_size[0]*0.7,fig_size[1])
#------------------
#BASE
Vin_min, Vin_max = 0,1.5 # [V]
I_min, I_max = 0,1500e-6 # [μA]
I=np.linspace(I_min,I_max,npt)
V = np.linspace(0,1,npt)
Vlhs = Vb0-Rb*I # equação LHS
ax0 = ax[1]
if ii==0:
ax0.plot(Vlhs,I*1e6,c=colors[ii],label = r'$V_{BB}-R_B I_B-V_{BE}(I_B)=0$')
ax0.plot(V, Ib(V)*1e6, c='gray',lw=2, label = r'$I_B(V_{BE})$',zorder=4)
else:
ax0.plot(Vlhs,I*1e6,c=colors[ii])
#solução para corrente e tensão
Vd = Vdiodob(Vb0,Vb0,Rb) # equação RHS
Id = Ib(Vd)
# ax0.axhline(1e6*Id, c='k', ls = '--',zorder=0)
# ax0.axvline(Vd, c='k', ls = '--',zorder=0)
lab = r'$I_B$,$V_{BE}$'+'={:2.0f} μA, {:2.0f} mV'.format(1e6*Id,1e3*Vd)
ax0.scatter(Vd,1e6*Id, c=colors[ii], marker='o', s=100)
#---
#lab = '$V_{aberto}$'+'={} V'.format(Vb0)
ax0.scatter(Vb0,0, color='b', marker='o', s=70,zorder=3)
#lab = '$I_{curto}$'+'={:2.1f} mA'.format(1e6*Vin/Rb)
ax0.scatter(0,Vb0/Rb*1e6, color='b', marker='P', s=70,zorder=3)
#---
#eixos x-y
ax0.axhline(0, color='k', linestyle = '-',lw=2)
ax0.axvline(0, color='k', linestyle = '-',lw=2)
#-----------------------
ax0.set_xlabel('Tensão, $V_{BE}$ (V)')
ax0.set_ylabel('Corrente, $I_B$ (μA)')
ax0.set_xlim([Vin_min,Vin_max])
ax0.set_ylim(np.array([I_min,I_max])*1e6)
ax0.legend(loc = 'lower center',bbox_to_anchor=[0.5,1.0])
ax0.grid(True,which='both')
ax0 = ax[2]
#------------------
#COLETOR_EMISSOR
Vbe = Vd # from previous
#limites dos eixos
Vin_min, Vin_max = -1,10 # [V]
I_min, I_max = -1,100 # [mA]
#-------------
V = np.linspace(0,10,npt)
#I = Idiodo(V) # equação diodo
I=np.linspace(I_min,I_max,npt)
#----------------------
Vlhs = Vin-Rc*I # equação LHS
#Vlhs = Vin-R*Id # equação LHS
#Vrhs = Vdiodo(Vin,Vin,R) # equação RHS
if ii==0:
ax0.plot(Vlhs,I*1e3,c='gray' ,label = r'$V_{CC}-R_C I_C-V_{CE}(I_C)=0$')
ax0.plot(V, Ic(V)*1e3, c=colors[ii],lw=2,label = r'$I_C(V_{CE})$',zorder=4)
else:
#ax0.plot(Vlhs,I*1e3)
ax0.plot(V, Ic(V)*1e3,c=colors[ii],lw=2,zorder=4)
#---
#eixos x-y
ax0.axhline(0, color='k', linestyle = '-',lw=2)
ax0.axvline(0, color='k', linestyle = '-',lw=2)
#---
#lab = '$V_{aberto}$'+'={} V'.format(Vin)
ax0.scatter(Vin,0, color='b', marker='o', s=70,zorder=3)
#lab = '$I_{curto}$'+'={:2.1f} mA'.format(1e3*Vin/Rc)
ax0.scatter(0,Vin/Rc*1e3, color='b', marker='P', s=70,zorder=3)
#solução para corrente e tensão
Vd = Vdiodo(Vin,Vin,Rc) # equação RHS
Id = Ic(Vd)
# ax0.axhline(1e3*Id, c='k', ls = '--',zorder=0)
# ax0.axvline(Vd, c='k', ls = '--',zorder=0)
lab = r'$I_C$,$V_{CE}$'+'={:2.0f} mA, {:2.0f} V'.format(1e3*Id,Vd)
ax0.scatter(Vd,1e3*Id, c=colors[ii], marker='o', s=100)
#-----------------------
ax0.set_xlabel('Tensão, $V_{CE}$ (V)')
ax0.set_ylabel('Corrente, $I_C$ (mA)')
ax0.set_xlim([Vin_min,Vin_max])
ax0.set_ylim([I_min,I_max])
ax0.legend(loc = 'lower center',bbox_to_anchor=[0.5,1.0])
ax0.grid(True,which='both')
ax0.xaxis.set_major_locator(plticker.MultipleLocator(2))
ax0.yaxis.set_major_locator(plticker.MultipleLocator(10))
#ax0.xaxis.set_major_locator(plticker.MultipleLocator(1))
#ax0.yaxis.set_major_locator(plticker.MultipleLocator(2))
plt.tight_layout()
return fig
vbbvec=np.arange(0.4,1.8,0.4)
fig = plot_ic_curves_transistor(Vcc=10,Rc=100,Vbb_vec=vbbvec,Rb=1000)
glue("fig_ic_ib_curves",fig,display=False)
glue("vbbvec",print(vbbvec))
[0.4 0.8 1.2 1.6]
None
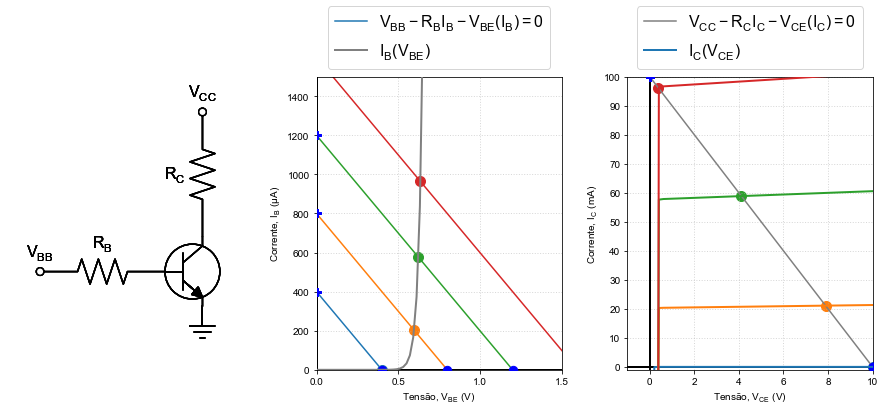
In order to solve the simple transistor circuit illustrated above, we must write Kirchhoff’s law for both base and collector meshes:
For the base mesh,
For the colector mesh,
In the active regime of the transistor (\(V_{BE}\geq 0.7\) V and \(V_{CE}>V{BE}\)), a simple relation is valid between \(I_C\) and \(I_B\) that couples base and collector meshes,
Althout it might seem rather straightforward to solve (),(), and eq:ic_bc the terms \(V_{BE}(I_B)\) and V_{CE}(I_C)$ are nonlinear functions that turn their solution into a rather complex task.
One way to proceed is to rely on graphical solutions, also known as load-lines methods, provided graphs of \(V_{BE}(I_B)\) and \(V_{CE}(I_C)\) are given. The essentials of this method are illustrated in fig:transistor_gif.
There are two revelant sets of load-lines, one for the base, \( I_B \) by the base loop circuit,
Clearly, this is a straight line in a \(I_B\times V_{BE}\) diagram, the slope is \(1/R_B\) and y-intercept \(I_B(0)=\cfrac{V_{BB}}{R_B}\).
The load curve that characterizes the transistor relates the value of \( I_C \) versus \( V_ {CE} \). Note that \( I_C = \beta I_B \), where \( \beta \) is defined by the transistor and
The value of \( V_ {CE} \) is defined by the collector’s mesh by the relation: $\( V_{CE} = V_{CC} - R_C I_C = V_{CC} - R_C (\beta I_B)\)$
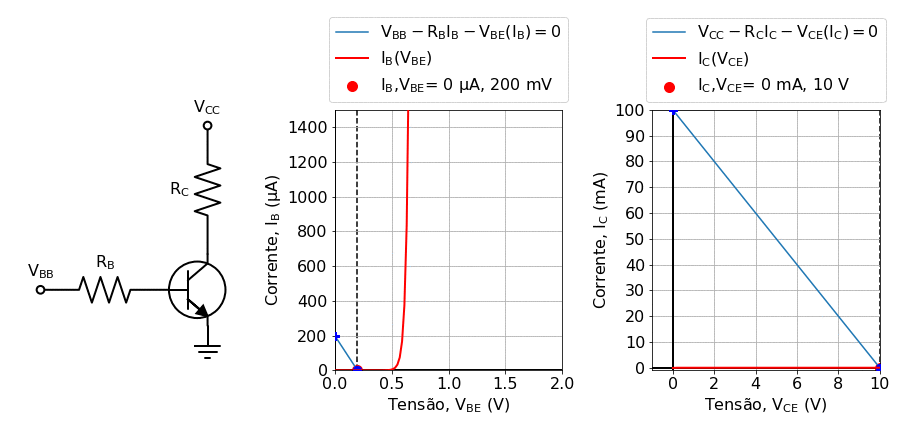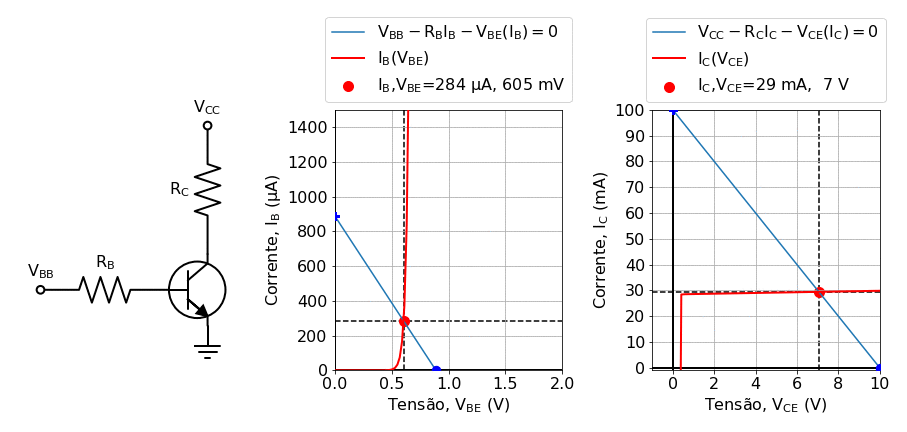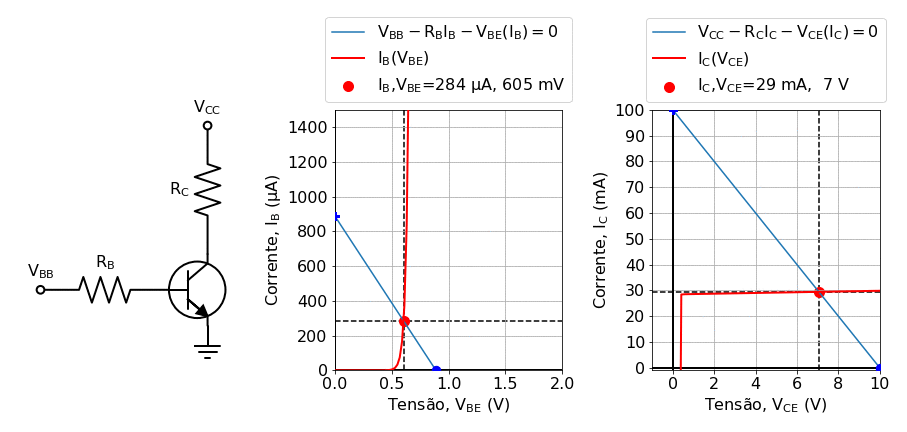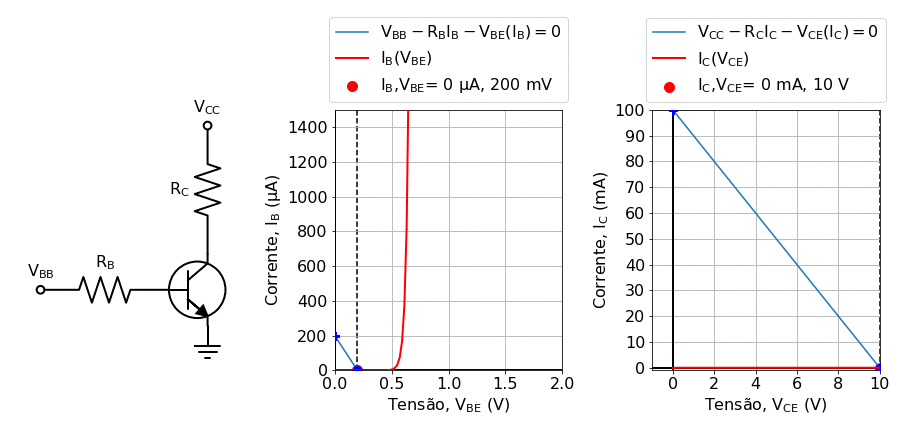
Fig. 19 Solving the transistor using the load line method for varying values of the base current. In this animation, generated in the notebook Background: Solving Kirchhoof’s law for transistors using load lines, the base voltage \(V_BB\) was varied in the range \(0.2 V\leq V_B\leq 1.2 V\).¶
We can see in these relations that for each value of \( I_B \) we have a value of \( I_C \) independent of \( R_C \) and \( V_ {CC} \). In this case, we will have load curves that are plateaus called active operating regions delimited by two regions. On the left (lower \(V_{CE}\)), a region where the reverse polarization of the base-collector diode occurs. On the right (higher \(V_{CE}\)) is the rupture region, where the very large voltages may permanently damage teh transistor.
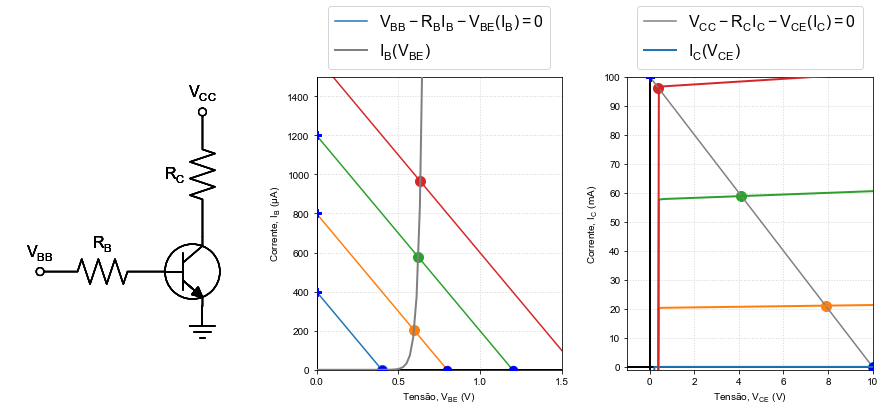
Fig. 20 \(I_C\) curves using \(V_BB=\)None V.¶
when \( V_ {CE} \) is between 0 and 1 V, the base-collector diode is not reverse polarized and therefore \( I_C \rightarrow \) 0 A to \( V_ {CE} \rightarrow \) 0 V, growing exponentially as a function of \( V_ {CE} \): saturation region;
\( I_C (= \beta I_B) \) is almost constant for a range of \( V_ {CE} \) forming a plateu: active regions;
transistor rupture region.
