Background: Complex impedances¶
Goals
Familiarizar com ondas senoidais e suas propriedades: amplitude, fase, frequência e período
Entender os casos mais comuns de controle de fluxo em programas em Python
Fazer gráficos elementares utilizando o pacote Matplotlib
Loading packages¶
import numpy as np
import os
import matplotlib.pyplot as plt
Setting up default matplotlib plotting parameters
#****************************
#GRAFICOS
#****************************
#Ajsutando fontes padrão dos gráficos
font = { 'weight' : 'normal',
'size' : 12}
plt.rc('font', **font)
#Ajsutando espessura das linhas padrão dos gráficos
plt.rcParams['lines.linewidth'] = 2;
Defining basic functions¶
#****************************
#FUNÇÃO PARA GRAFICAR DIAGRAMA DE ARGAND (PLANO COMPLEXO)
#****************************
def z_plot(zlist,scale_factor=1.1):
''' FUNÇÃO PARA GRAFICAR NÚMERO COMPLEXO NO DIAGRAMA DE ARGAND, CARTESIANO E POLAR
entrada:
zlist = lista contendo um ou mais números (array ou numpy.array)
obs: se quiser apenas um número, coloque colchetes, [z]
scale_factor (opcional) = fator de escala para definir o excesso dos eixos
saída: figura matplotlib
'''
fig, ax = plt.subplots(2, figsize=(10,5));
#----------------------
#GRÁFICO CARTESIANO
ax[0] = plt.subplot(1,2,1) # primeiro grafico de uma matrix 1x2
for z in zlist:
ax[0].plot([0,z.real],[0,z.imag],'.--k'); # desenha uma linha tracejada da origem até ponto
ax[0].plot(z.real,z.imag,'o',markersize = 10) #desenha o ponto
zmax = scale_factor*np.max(np.abs(zlist))
ax[0].plot(zmax*np.array([0,0]),zmax*np.array([-1,1]),'-k')#eixos cartesianos
ax[0].plot(zmax*np.array([-1,1]),zmax*np.array([0,0]),'-k')#eixos cartesianos
ax[0].set_xlim([-zmax,zmax]);
ax[0].set_ylim([-zmax,zmax]);
ax[0].set_xlabel('parte real');
ax[0].set_ylabel('parte imaginária');
plt.title('Diagrama de Argand');
ax[0].grid(True);
#----------------------
#GRÁFICO POLAR
ax[1] = plt.subplot(1,2,2,projection='polar') # primeiro grafico de uma matrix 1x2
count = 1
for z in zlist:
ax[1].plot([0,np.angle(z)],[0,np.abs(z)],'.--k'); # desenha uma linha tracejada da origem até ponto
ax[1].plot(np.angle(z),np.abs(z),'o', markersize = 10, label = 'z'+str(count)) #desenha o ponto
count = count+1
#ax[1].set_rmax(scale_factor*np.array([-np.abs(z),np.abs(z)]));
# plt.title('Forxma polar');
ax[1].grid(True);
ax[1].set_rlabel_position(0)
ax[1].set_rmax(zmax)
ax[1].set_xticks(np.pi/180. * np.linspace(180, -180, 8, endpoint=False))
ax[1].set_thetalim(-np.pi, np.pi)
#ax[1].legend(loc='lower right')
ax[1].legend(loc=(1.2,0.45))
return fig; # retorna a figura
#-------------------------------------------
#****************************
#FUNÇÃO PARA GRAFICAR DIAGRAMA DE BODE (|H|**2 E ARG(H)
#****************************
def fig_bode(freq,Tdbvec,fasevec,labelvec):
'''Função para graficar painel 2x1 com diagrama de Bode (amplitude e fase)
entrada:
freq (vetor numérico de frequência)
Tdbvec (vetor numérico)
'''
fig, ax = plt.subplots(2, sharex=True, figsize=(5, 10));
#--------------------------------------
#TRANSMITANCIA EM DECIBEIS
ax[0] = plt.subplot(211)
for m in range(np.shape(Tdbvec)[0]):
ax[0].plot(freq,np.array(Tdbvec)[m,:],'-*',linewidth=2,label=labelvec[m])
#ax[0].plot(freq,np.array(Tdbvec)[m,:],,label=labelvec[m])
ax[0].set_ylim((-40,30))
ax[0].set_xscale('log')
ax[0].set_ylabel('T (dB)')
ax[0].legend(loc='lower right')
ax[0].grid(True)
#--------------------------------------
ax[1] = plt.subplot(212)
for m in range(np.shape(fasevec)[0]):
ax[1].plot(freq,np.array(fasevec)[m,:],'-*',linewidth=2,label=labelvec[m])
ax[1].set_ylim([-200,200])
ax[1].set_xscale('log')
ax[1].set_ylabel('Fase (graus)')
ax[1].grid(True)
#--------------------------------------
#geral
ax[0].set_title('Diagrama de Bode')
plt.xlabel('Frequência (Hz)')
return fig
Impedâncias complexas no Python¶
Abaixo, definimos as impedâncias complexas para o capacitor, para o capacitor: $\(Z_c=-j X_c=-j \frac{1}{\omega C}=-j \frac{1}{2\pi f C},\)\( sendo \)f$ a frequência (em [Hz]).
Para o indutor, $\(Z_l=j X_l=j \omega L=j 2\pi f L,\)\( sendo \)f$ a frequência (em [Hz]).
A seguir são definidas funções de Python que calculam as impedâncias complexas para um capacitor e um indutor
#-----------------
#CAPACITOR
def Zc(freq,C):
#reatancia
Xc = 1/(2*np.pi*freq*C)
#impedancia complexa
Zc = -1j*Xc
return Zc
#-----------------
#INDUTOR
def Zl(freq,L):
#reatancia
Xl = 2*np.pi*freq*L
#impedancia complexa
Zl = 1j*Xl
return Zl
A impedância de cada um dos componentes é puramente reativo, não possui parte real:
Pergunta: Quais os valores possíveis para a fase das impedâncias de componentes puramente reativos?
#definindo valores dos componentes
freq = 500 # frequencia [Hz]
C = 90e-6; #capacitancia [F]
L = 10e-3; # indutancia [H]
#calculando
print('impedância complexa capacitor, Zc= {:1.1g}'.format(Zc(freq,C)))
print(Zl(freq,L))
#graficando:
test=z_plot([Zc(freq,C),Zl(freq,L)])
impedância complexa capacitor, Zc= 0-4j
31.41592653589793j
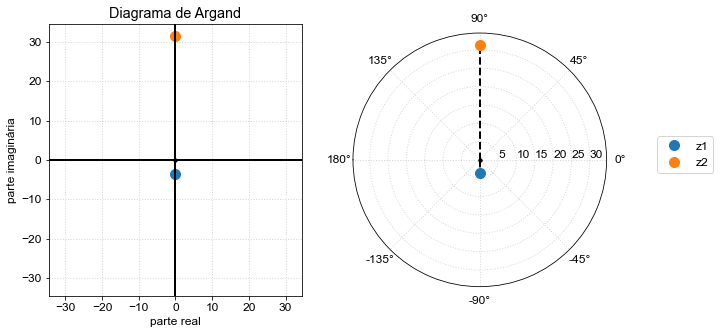
Para visulizar a relação entre as impedância complexas acima e o que se observa em um osciloscópio, basta tomarmos a parte real do sinal complexo. Suponha que tenhamos uma corrente \(I(t)=i_0 \cos(\omega t+\phi)\) no nosso circuito. A corrente complexa associada será $\( \tilde{I}(t)=i_0 \exp(j\omega t+\phi)=\tilde{i}_0\exp(j\omega t), \)\( (eq:complex_current) sendo que \)\tilde{i}_0=i_0\exp(j\phi)$
freq = 10 # frequencia [Hz]
L = 10e-3; # indutancia [H
#---
time= np.linspace(0,3/freq,100) # time vector
omega=2*np.pi*freq # 1 kHz frequency
c_current = np.exp(1j*omega*time) # complex current
c_voltage = Zl(freq,L)*c_current # complex voltage
#---
current = np.real(c_current) # real current
voltage = np.real(c_voltage) # real voltage
#---
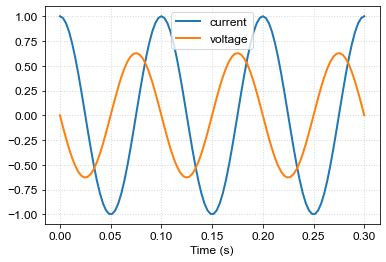
plt.plot(time,current,label='current')
plt.plot(time,voltage,label='voltage')
plt.xlabel('Time (s)')
plt.grid(True)
plt.legend()
<matplotlib.legend.Legend at 0x7f90311fff50>
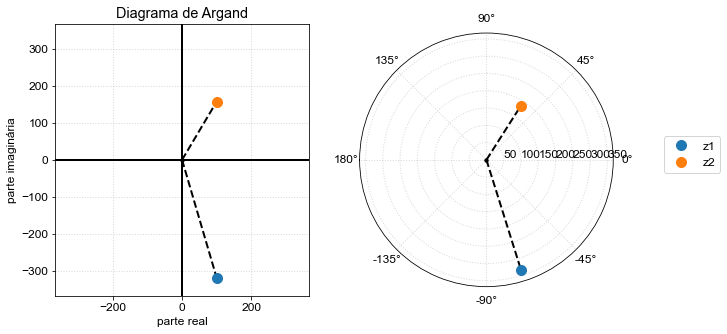
Já para o circuito \(RC\) ou \(RL\) série, a impedância total possui parte real e imaginária. Note que o \(RC\) possui parte imaginária negativa (\(\mathcal{Im}(Z)<0\), capacitivo) e o \(RL\) possui parte imaginária positivo (\(\mathcal{Im}(Z)>0\), indutivo),
#definindo valores dos componentes
freq = 500 # frequencia [Hz]
C = 1e-6; #capacitancia [F]
L = 50e-3; # indutancia [H]
R = 100; #resistencia [Ohms]
#impedancia total de um circuito RC ou RL
print(R + Zc(freq,C))
print(R + Zl(freq,L))
#graficando:
z_plot([R+Zc(freq,C),R+Zl(freq,L)]);
(100-318.3098861837907j)
(100+157.07963267948966j)
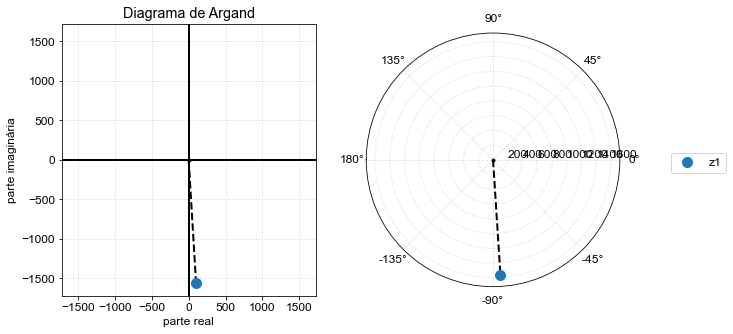
Já para o circuito \(RLC\) série, dependendo da frequência, ele pode ser mais indutivo \(\mathcal{Im}(Z)>0\) ou capacitivo \(\mathcal{Im}(Z)<0\). Altere o valor da frequência (freq) e verifique este comportamento.
#definindo valores dos componentes
freq = 100 # frequencia [Hz]
C = 1e-6; #capacitancia [F]
L = 50e-3; # indutancia [H]
R = 100; #resistencia [Ohms]
#impedancia total de um circuito RC ou RL
print(R + Zl(freq,L) + Zc(freq,C))
z_plot([R + Zl(freq,L) + Zc(freq,C)]);
(100-1560.1335043830557j)
Forma polar¶
Note a importância de usar a função np.angle (argumento), ao invés de usar o np.arctan (arco-tangente)¶
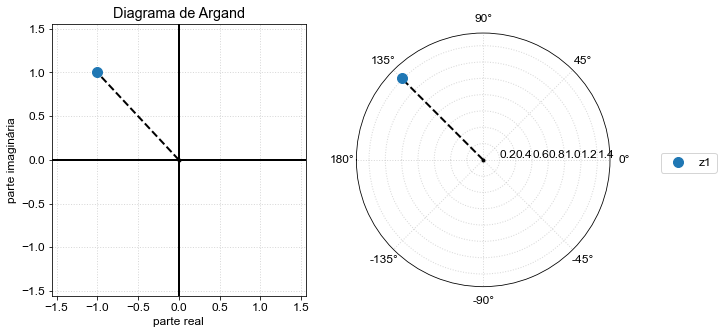
No primeiro quadrante…
z = -1 + complex(0,1)
print(z)
print(z.real)
print(z.imag)
#calculando a fase (em graus):
fase_atan = (180/np.pi)*np.arctan(z.imag/z.real)
print(fase_atan)
fase_angle = (180/np.pi)*np.angle(z)
print(fase_angle)
#graficando
z_plot([z]);
(-1+1j)
-1.0
1.0
-45.0
135.0
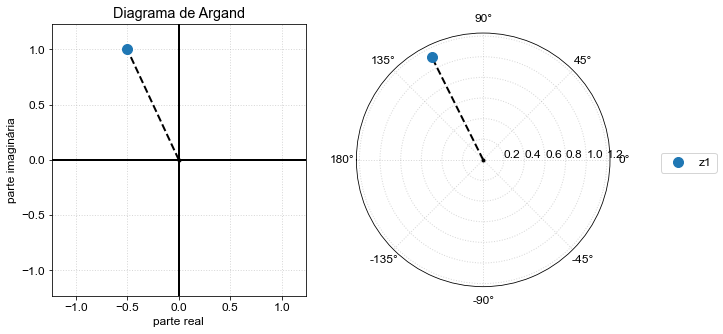
No segundo quadrante…
z = -0.5 + complex(0,1)
print(z)
print(z.real)
print(z.imag)
#calculando a fase (em graus):
fase_atan = (180/np.pi)*np.arctan(z.imag/z.real)
print(fase_atan)
fase_angle = (180/np.pi)*np.angle(z)
print(fase_angle)
#graficando
z_plot([z]);
(-0.5+1j)
-0.5
1.0
-63.43494882292202
116.56505117707799
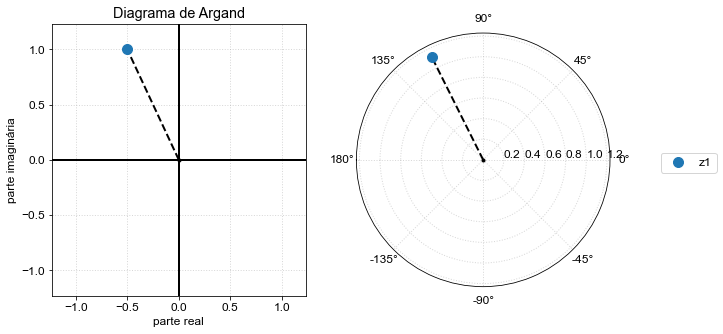
Convertendo entre as duas formas:¶
sendo que \(\theta=arg(z)\)
z = -0.5 + complex(0,1)
print('forma cartesiana:',z)
print('parte real:',z.real)
print('parte imaginaria:',z.imag)
#fase
theta = np.angle(z)
print('fase (rad)',theta)
#modulo
zabs = np.abs(z)
print('módulo',zabs)
#FORMA POLAR
j=complex(0,1)
zpolar = zabs* np.exp(j*theta)
print('forma polar:',zpolar)
#---------------------------------------
#Grafico representando o número complexo
#graficando
z_plot([z]);
forma cartesiana: (-0.5+1j)
parte real: -0.5
parte imaginaria: 1.0
fase (rad) 2.0344439357957027
módulo 1.118033988749895
forma polar: (-0.5+1j)
j=complex(0,1)
r1, theta1 = 1.5, np.pi/2
r2, theta2 = 1.0, np.pi/4
z1 = r1*np.exp(j*theta1)
z2 = r2*np.exp(j*theta2)
z3 = z1*z2
z4 = z2/z1
z_plot([z1,z2,z3,z4]);
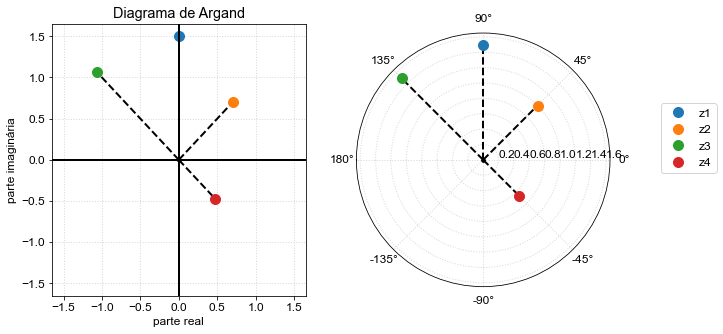
Graficando as impedâncias dos componentes reativos¶
freq=np.linspace(10,1000,500) # vetor que vai de 10**0 até 10**6
C=5e-6;
L=100e-3;
#-----
#GRAFICOS
#Ajsutando fontes padrão dos gráficos
font = {'family' : 'arial',
'weight' : 'normal',
'size' : 16} #este tipo de variável é um dicionário
plt.rc('font', **font)
plt.rcParams['lines.linewidth'] = 2
#Ajsutando espessura das linhas padrão dos gráficos
#IMPEDÂNCIA,|Z|
fig, ax = plt.subplots(2,figsize=(14, 5))
ax[0] = plt.subplot(121)
ax[0].plot(freq,np.abs(Zl(freq,L)),label='indutor')
ax[0].plot(freq,np.abs(Zc(freq,C)),label='capacitor')
#nome dos eixos e legendas
ax[0].set_xlabel('Frequência (Hz)')
ax[0].set_ylabel('Impedância (Ohms)')
ax[0].legend(loc='upper right')
#-----
#FASE,arg(Z)
ax[1] = plt.subplot(122)
ax[1].plot(freq,np.angle(Zl(freq,L),deg=True),label='indutor')
ax[1].plot(freq,np.angle(Zc(freq,C),deg=True),label='capacitor')
#nome dos eixos e legendas
ax[1].set_xlabel('Frequência (Hz)')
ax[1].set_ylabel('Fase (graus)')
ax[1].legend(loc='center right')
<matplotlib.legend.Legend at 0x7f9031b67b10>
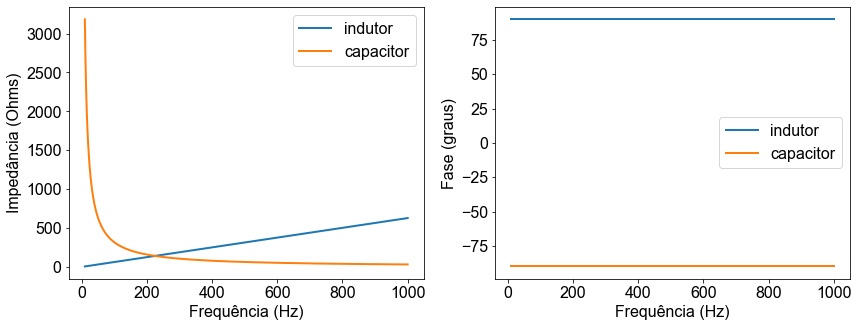
Circuitos contendo 1 componentes reativos, RC e RL¶
Abaixo definimos uma função para fazer diagramas de Bode¶
circuito RC¶
freq=np.logspace(1,6,20) # vetor que vai de 10**0 até 10**6
#lomega=np.log10(omega)
C=1e-3;
L=1e-3/(2*np.pi)**2;
R=0.2;
#----------------
Zt = Zc(freq,C)+R # impedancia total
Hrc = Zc(freq,C)/Zt # H com capacitor na saida
Hcr = R/Zt # H com resistor na saida
#----------------
Trc=np.abs(Hrc)
Trcdb=20*np.log10(Trc)
fase_rc = np.angle(Hrc,deg=True)
#capacitor
Tcr=np.abs(Hcr)
Tcrdb=20*np.log10(Tcr)
fase_cr = np.angle(Hcr,deg=True)
#GRAFICANDO BODE, RC e CR
fig=fig_bode(freq,[Trcdb,Tcrdb],[fase_rc,fase_cr],['C','R']);
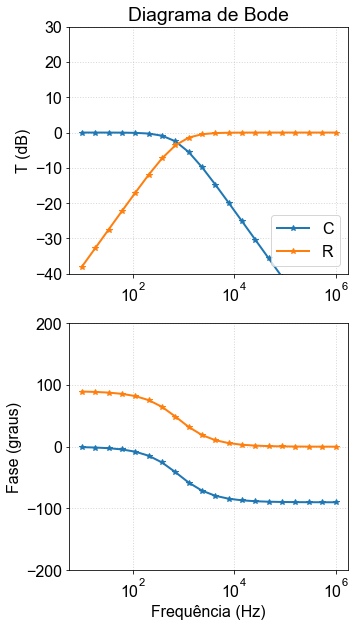
#SALVANDO FIGURA
#-----------------------------
print('pasta atual:',os.getcwd())
name='bode_rc'
folder_path=os.getcwd()
ext='pdf'
path=os.path.join(folder_path,name + '.' + ext)
fig.savefig(path,format='pdf')
print('arquivo salvo:',path)
pasta atual: /Users/gsw/GitHub/F540_jbook/guides/exp1
arquivo salvo: /Users/gsw/GitHub/F540_jbook/guides/exp1/bode_rc.pdf
circuito RL¶
freq=np.logspace(0,6,200) # vetor que vai de 10**0 até 10**6
#lomega=np.log10(omega)
C=1e-3;
L=1e-3/(2*np.pi)**2;
R=0.2;
#----------------
Zt = Zl(freq,L)+R
Hrl,Hlr = Zl(freq,L)/Zt, R/Zt
#----------------
Trl=np.abs(Hrl)
Trldb=20*np.log10(Trl)
fase_rl = np.angle(Hrl,deg=True)
#capacitor
Tlr=np.abs(Hlr)
Tlrdb=20*np.log10(Tlr)
fase_lr = np.angle(Hlr,deg=True)
#GRAFICANDO BODE, LR e RL
fig=fig_bode(freq,[Trldb,Tlrdb],[fase_rc,fase_cr],['L','R']);
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-19-ad4efcaf4902> in <module>
1 #GRAFICANDO BODE, LR e RL
----> 2 fig=fig_bode(freq,[Trldb,Tlrdb],[fase_rc,fase_cr],['L','R']);
<ipython-input-3-93398a12e94a> in fig_bode(freq, Tdbvec, fasevec, labelvec)
69 ax[1] = plt.subplot(212)
70 for m in range(np.shape(fasevec)[0]):
---> 71 ax[1].plot(freq,np.array(fasevec)[m,:],'-*',linewidth=2,label=labelvec[m])
72 ax[1].set_ylim([-200,200])
73 ax[1].set_xscale('log')
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/matplotlib/axes/_axes.py in plot(self, scalex, scaley, data, *args, **kwargs)
1741 """
1742 kwargs = cbook.normalize_kwargs(kwargs, mlines.Line2D)
-> 1743 lines = [*self._get_lines(*args, data=data, **kwargs)]
1744 for line in lines:
1745 self.add_line(line)
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/matplotlib/axes/_base.py in __call__(self, data, *args, **kwargs)
271 this += args[0],
272 args = args[1:]
--> 273 yield from self._plot_args(this, kwargs)
274
275 def get_next_color(self):
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/matplotlib/axes/_base.py in _plot_args(self, tup, kwargs)
397
398 if x.shape[0] != y.shape[0]:
--> 399 raise ValueError(f"x and y must have same first dimension, but "
400 f"have shapes {x.shape} and {y.shape}")
401 if x.ndim > 2 or y.ndim > 2:
ValueError: x and y must have same first dimension, but have shapes (200,) and (20,)
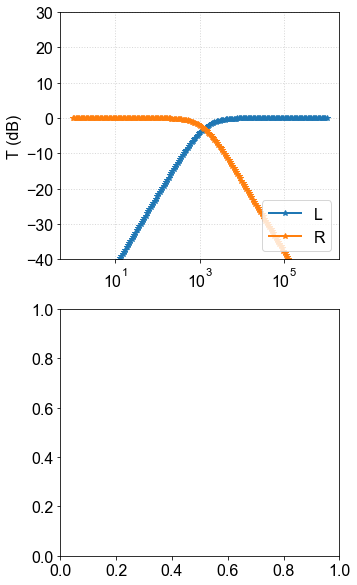
#SALVANDO FIGURA
#-----------------------------
print('pasta atual:',os.getcwd())
name='bode_rl'
folder_path=os.getcwd()
ext='pdf'
path=os.path.join(folder_path,name + '.' + ext)
fig.savefig(path,format='pdf')
print('arquivo salvo:',path)
Circuitos contendo 2 componentes reativos, RLC¶
freq=np.logspace(0,6,500) # vetor que vai de 10**0 até 10**6
#lomega=np.log10(omega)
C=1e-3;
L=1e-3/(2*np.pi)**2;
R=0.1;
#----------------
Zt = Zc(freq,C)+Zl(freq,L)+R # impedancia total
Hr = R/Zt # resistor na saida
Hc = Zc(freq,C)/Zt # capacitor na saida
Hl = Zl(freq,L)/Zt # indutor na saida
Hlc = (Zc(freq,C)+Zl(freq,L))/Zt # indutor e capacitor na saida
#----------------
Tr=np.abs(Hr)
Trdb=20*np.log10(Tr)
fase_r = np.angle(Hr,deg=True)
#capacitor
Tc=np.abs(Hc)
Tcdb=20*np.log10(Tc)
fase_c = np.angle(Hc,deg=True)
#indutor
Tl=np.abs(Hl)
Tldb=20*np.log10(Tl)
fase_l = np.angle(Hl,deg=True)
#indutor+capacitor
Tlc=np.abs(Hlc)
Tlcdb=20*np.log10(Tlc)
fase_lc = np.angle(Hlc,deg=True)
fig=fig_bode(freq,[Trdb,Tcdb,Tldb,Tlcdb],[fase_r,fase_c,fase_l,fase_lc],['R','L','C','LC']);
#-----------------------------
print('pasta atual:',os.getcwd())
name='bode_rlc'
folder_path=os.getcwd()
ext='pdf'
path=os.path.join(folder_path,name + '.' + ext)
fig.savefig(path,format='pdf')
print('arquivo salvo:',path)
