Solving Kirchhoff’s law ordinary differential equation¶
Import packages…
from sympy import *
#pacote para desenhar circuitos
import SchemDraw as schem
import SchemDraw.elements as e
d = schem.Drawing(unit=2.5)
d.add(e.DOT_OPEN, label ='$V_{in}$')
comp1 =d.add(e.RES, d='right',label='$R$') #capacitor
d.add(e.CAP, d='down',label='$C$') # resistor de saída
d.add(e.GND)
#output
d.add(e.LINE, d='right', xy=comp1.end, l=1)
d.add(e.DOT_OPEN,label ='$V_{out}$')
#---
d.draw()
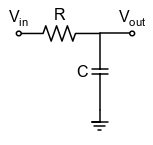
Escrevendo a lei de Kirchhoff para o circuito da figura acima,
(1)¶\[\frac{dq}{dt}+\frac{1}{\tau}q=\frac{v_{in}(t)}{R}.\]
Exploraremos o pacote sympy para nos ajudar a resolver esta equação diferencial ordinária.
Defining symbols and equation to be solved¶
A solução tentantiva será na forma,
(2)¶\[ q(t)=A \cos(\omega t)+B\sin(\omega t)\]
A,B,omega,t, tau = symbols('A B omega t tau')
qtrial= A*cos(omega*t)+B*sin(omega*t)
lhs = diff(qtrial,t)+1/tau*qtrial
v0, R = symbols('v0 R')
rhs = v0/R*cos(omega*t)
eq = lhs-rhs
simplify(lhs)
\[\displaystyle \frac{A \cos{\left(\omega t \right)} + B \sin{\left(\omega t \right)} + \omega \tau \left(- A \sin{\left(\omega t \right)} + B \cos{\left(\omega t \right)}\right)}{\tau}\]
terms = [sin(omega*t),cos(omega*t)]
eqlhs=collect(simplify(eq),terms)
coefs = [eqlhs.coeff(term) for term in terms]
coefs
[-A*omega + B/tau, A/tau + B*omega - v0/R]
eq2 = [Eq(coef,0) for coef in coefs]
solution, = linsolve(eq2,(A,B))
sol = solution[0]*terms[0] + solution[1]*terms[1]
simplify(sol)
\[\displaystyle \frac{\tau v_{0} \left(\omega \tau \cos{\left(\omega t \right)} + \sin{\left(\omega t \right)}\right)}{R \left(\omega^{2} \tau^{2} + 1\right)}\]
print_latex(simplify(sol))
\frac{\tau v_{0} \left(\omega \tau \cos{\left(\omega t \right)} + \sin{\left(\omega t \right)}\right)}{R \left(\omega^{2} \tau^{2} + 1\right)}
Therefore, the solution is:
\[q(t) = \frac{\tau v_{0} \left(\omega \tau \cos{\left(\omega t \right)} + \sin{\left(\omega t \right)}\right)}{R \left(\omega^{2} \tau^{2} + 1\right)}
\]
Another form….¶
Equivalently we could solve directly for the electric current \(i=dq/dt\), $\(\frac{di}{dt}+\frac{1}{\tau}i=\frac{1}{R}\frac{d v_{in}(t)}{dt}\)$
i0 ,omega,t, tau, theta = symbols('i0 omega t tau theta')
itrial= i0*cos(omega*t+theta)
lhs = expand_trig(diff(itrial,t)+1/tau*itrial)
lhs
\[\displaystyle - i_{0} \omega \left(\sin{\left(\theta \right)} \cos{\left(\omega t \right)} + \sin{\left(\omega t \right)} \cos{\left(\theta \right)}\right) + \frac{i_{0} \left(- \sin{\left(\theta \right)} \sin{\left(\omega t \right)} + \cos{\left(\theta \right)} \cos{\left(\omega t \right)}\right)}{\tau}\]
v0, R = symbols('v0 R')
rhs = diff(v0/R*cos(omega*t),t)
eq = lhs-rhs
eq
\[\displaystyle - i_{0} \omega \left(\sin{\left(\theta \right)} \cos{\left(\omega t \right)} + \sin{\left(\omega t \right)} \cos{\left(\theta \right)}\right) + \frac{i_{0} \left(- \sin{\left(\theta \right)} \sin{\left(\omega t \right)} + \cos{\left(\theta \right)} \cos{\left(\omega t \right)}\right)}{\tau} + \frac{\omega v_{0} \sin{\left(\omega t \right)}}{R}\]
coefs = [expand(eq).coeff(term) for term in terms]
coefs
[-i0*omega*cos(theta) - i0*sin(theta)/tau + omega*v0/R,
-i0*omega*sin(theta) + i0*cos(theta)/tau]
eq2
[Eq(-A*omega + B/tau, 0), Eq(A/tau + B*omega - v0/R, 0)]
eq2 = [Eq(coef,0) for coef in coefs]
solution, = linsolve(eq2,(i0,theta))
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/polys/polyutils.py in _parallel_dict_from_expr_if_gens(exprs, opt)
209
--> 210 monom[indices[base]] = exp
211 except KeyError:
KeyError: cos(theta)
During handling of the above exception, another exception occurred:
PolynomialError Traceback (most recent call last)
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/solvers/solveset.py in linsolve(system, *symbols)
2638 try:
-> 2639 eqs, ring = sympy_eqs_to_ring(eqs, symbols)
2640 except PolynomialError as exc:
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/polys/solvers.py in sympy_eqs_to_ring(eqs, symbols)
127 try:
--> 128 K, eqs_K = sring(eqs, symbols, field=True, extension=True)
129 except NotInvertible:
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/polys/rings.py in sring(exprs, *symbols, **options)
162 # TODO: rewrite this so that it doesn't use expand() (see poly()).
--> 163 reps, opt = _parallel_dict_from_expr(exprs, opt)
164
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/polys/polyutils.py in _parallel_dict_from_expr(exprs, opt)
330 if opt.gens:
--> 331 reps, gens = _parallel_dict_from_expr_if_gens(exprs, opt)
332 else:
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/polys/polyutils.py in _parallel_dict_from_expr_if_gens(exprs, opt)
215 raise PolynomialError("%s contains an element of "
--> 216 "the set of generators." % factor)
217
PolynomialError: cos(theta) contains an element of the set of generators.
During handling of the above exception, another exception occurred:
NonlinearError Traceback (most recent call last)
<ipython-input-18-6ed066c8a656> in <module>
1 eq2 = [Eq(coef,0) for coef in coefs]
----> 2 solution, = linsolve(eq2,(i0,theta))
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sympy-1.7.1-py3.7.egg/sympy/solvers/solveset.py in linsolve(system, *symbols)
2640 except PolynomialError as exc:
2641 # e.g. cos(x) contains an element of the set of generators
-> 2642 raise NonlinearError(str(exc))
2643
2644 try:
NonlinearError: cos(theta) contains an element of the set of generators.
sol = solution[0]*terms[0] + solution[1]*terms[1]
simplify(sol)
\[\displaystyle \frac{\omega \tau v_{0} \left(\omega \tau \sin{\left(\omega t \right)} - \cos{\left(\omega t \right)}\right)}{R \left(\omega^{2} \tau^{2} + 1\right)}\]
We can write the solution above in a simpler form by noting
