Plotting: Interactive analysis of an RLC ressonant filter¶
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interactive
import matplotlib
font = {'family' : 'arial',
'weight' : 'normal',
'size' : 18}
matplotlib.rc('font', **font)
Filtro RLC passa-banda¶
A função resposta de um filtro RLC com resistor na saída será dada por, $\(H=\frac{R}{R+Z_L+Z_C}\)\( Na expressão acima, \)Z_L\( e \)Z_C$ representam as impedâncias complexas do indutor e capacitor.
Capacitor e Indutor ideais¶
Neste caso, \(Z_L=jX_L\) e \(Z_C=-jX_C\), sendo que as as reatâncias são dadas por \(X_L=\omega L\) e \(X_C=1/(\omega C)\) $\(H=\frac{R}{R+j(X_L-X_C)}\)$
def T(freq,R,L,C):
#função para gerar transmitância
ω = 2*np.pi*freq
XL = ω*L
XC = 1/(ω*C)
H = R/(R+1j*(XL-XC))
return np.abs(H)**2
#---
#grafico básico
freq = np.linspace(10,1e4,200)
plt.plot(freq,T(freq,100,50e-3,220e-9))
plt.show()
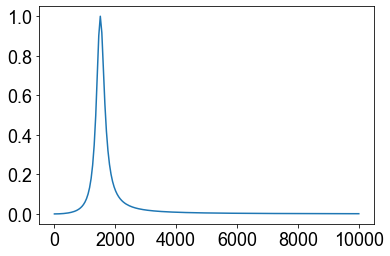
Abaixo geramos um gráfico dentro de uma função plot_interactive1(R=1e2,L=50,C=220) que nos pemitirá gerar um gráfico interativo, nos quais os três argumentos da função R,L,C serão controlados.
def plot_interactive1(R=1e2,L=50,C=220):
#Esta função gera o grafico com base nos parâmetros R,L,C
#Unidades: R[Ω]; L[mH]; C[nF]
#-------
L = L*1e-3 #converte para H
C = C*1e-9 # converte para F
f0 = 1/(2*np.pi*np.sqrt(L*C)) # ressonancia
f1 = ((1/2)*((C**-1)*((L**-1)*((C*R)+((C**(1/2))*(((4*L)+(C*(R**2)))**(1/2))))))) /(2*np.pi)
f2 = ((1/2)*((C**-1)*((L**-1)*((-1*(C*R))+((C**(1/2))*(((4*L)+(C*(R**2)))**(1/2))))))) /(2*np.pi)
#---graficos
fig, ax = plt.subplots(1,2,figsize=(12,4))
#---------------
#eixo da esquerda
#---------------
ax[0].plot(freq,T(freq,R,L,C)) # transmitância
ax[0].plot(freq,0*freq+0.5,'--k') #meia-altura
ax[0].plot([f1,f0, f2],[T(f1,R,L,C),T(f0,R,L,C),T(f2,R,L,C)],'or')# pontos da largura meia altura
#formatação do gráfico
ax[0].set_xlabel('Frequência (Hz)')
ax[0].set_ylabel('Transmitância')
ax[0].set_xlim([10,1e4])
ax[0].set_ylim([0,1.1])
ax[0].grid(True)
#---------------
#eixo da direita
#---------------
ax[1].plot(freq,10*np.log10(T(freq,R,L,C)))
ax[1].plot(freq,0*freq-3,'--k')
ax[1].plot([f1, f2],10*np.log10([T(f1,R,L,C),T(f2,R,L,C)]),'or')
#formatação do gráfico
ax[1].set_xlabel('Frequência (Hz)')
ax[1].set_ylabel('Transmitância (dB)')
ax[1].set_xlim([10,1e4])
ax[1].set_ylim([-30,0.5])
ax[1].grid(True)
plt.xscale('log')
plt.tight_layout()
plt.show()
freq = np.linspace(10,1e4,200)
graph1 = interactive(plot_interactive1,R=(1e2,1e3,100),L=(10,100,10),C=(100,800,100))
graph1
Indutor com resistência interna (em série),¶
Neste caso, \(Z_L=r_L+jX_L\) e \(Z_C=-jX_C\), sendo que as as reatâncias são dadas por \(X_L=\omega L\) e \(X_C=1/(\omega C)\) $\(H=\frac{R}{R+r_l+j(X_L-X_C)}\)$
def T(freq,R=1e2,rl=0,L=50,C=220):
ω = 2*np.pi*freq
XL = ω*L
XC = 1/(ω*C)
H = R/(R+rl+1j*(XL-XC))
return np.abs(H)**2
def plot_interactive2(R=1e2,rl=0,L=50,C=220):
#Esta função gera o grafico com base nos parâmetros R,L,C
#Unidades: R[Ω]; L[mH]; C[nF]
L = L*1e-3 #converte para H
C = C*1e-9 # converte para F
f0 = 1/(2*np.pi*np.sqrt(L*C)) # ressonancia
f1 = ((1/2)*((C**-1)*((L**-1)*((C*R)+((C*rl)+(((4*(C*L))+(((-1*(C*R))+(-1*(C*rl)))**2))**(1/2)))))))/(2*np.pi)
f2 = ((1/2)*((C**-1)*((L**-1)*((-1*(C*R))+((-1*(C*rl))+(((4*(C*L))+(((C*R)+(C*rl))**2))**(1/2)))))))/(2*np.pi)
#---graficos
fig, ax = plt.subplots(1,2,figsize=(12,4))
#---------------
#eixo da esquerda
#---------------
ax[0].plot(freq,T(freq,R,rl,L,C))
ax[0].plot(freq,0*freq+T(f0,R,rl,L,C)/2,'--k')
ax[0].plot([f1, f0, f2],[T(f1,R,rl,L,C),T(f0,R,rl,L,C),T(f2,R,rl,L,C)],'or')
#formatação do gráfico
ax[0].set_xlabel('Frequência (Hz)')
ax[0].set_ylabel('Transmitância')
ax[0].set_xlim([10,1e4])
ax[0].set_ylim([0,1.1])
ax[0].grid(True)
#---------------
#eixo da direita
#---------------
ax[1].plot(freq,10*np.log10(T(freq,R,rl,L,C)))
ax[1].plot(freq,0*freq +10*np.log10(T(f0,R,rl,L,C))-3,'--k')
ax[1].plot([f1, f0, f2],10*np.log10([T(f1,R,rl,L,C),T(f0,R,rl,L,C),T(f2,R,rl,L,C)]),'or')
#formatação do gráfico
ax[1].set_xlabel('Frequência (Hz)')
ax[1].set_ylabel('Transmitância (dB)')
ax[1].set_xlim([10,1e4])
ax[1].set_ylim([-30,0.5])
ax[1].grid(True)
plt.xscale('log')
plt.tight_layout()
plt.show()
graph2 = interactive(plot_interactive2,R=(1e2,1e3,100),rl=(0,100,10),L=(10,100,10),C=(100,800,100))
freq = np.linspace(10,1e4,200)
graph2
